The Wind Load On Walls
Episode #5 of the Structural Loads Series
Hello friends, 🙋♂️🙋♂️
Today, we’ll look at how to calculate the horizontal wind load on walls. The horizontal wind loads have a different impact on the building as most other loads, which are vertical.
Vertical loads are taken up by beams, walls, slabs, and columns, which we are quite familiar with because 90% of our structural design courses focus on these elements. But university often doesn’t put enough time into horizontal load bearing systems / the stability of a building. Examples of stabilizing elements are wind braces, cores, frames, shear walls, but also floor diaphragms which transfer the loads from the facades to the stabilizing system which transfers the load down to the foundation.
Step-By-Step Process Of Calculating The Wind Load On Walls
In order to calculate the wind load or wind pressure on external surfaces, we are going to do the following steps:
Calculate the peak velocity pressure qp
Define the outer geometry of the building (width, height, length)
Calculate the width of the wind areas
Find the external pressure coefficients from Eurocode
Calculate the wind pressures/loads on the walls/facades
Example Building
We’ll use the same example building as last week to show all the steps of calculating the wind load on walls.
YouTube Video
If you prefer video, you can also check out this YouTube video that I made.
#1 Peak Velocity Pressure
We calculated the peak velocity pressure in last week’s episode as:
If you missed that newsletter, then you’ll find it → here ←.
#2 Define the outer geometry of the building (width, height, length)
The building has the following dimensions:
#3 Calculation Of The Width Of The Wind Areas
The wind load on walls is split up in 5 different areas according to EN 1991-1-4 Figure 7.5. If the building isn’t square, the wind areas are different when wind is blowing in longitudinal and transverse direction.
Wind in transverse direction
According to EN 11991-1-4, the width and length of the building (parameter d) for wind in transverse direction are defined as following:
From those dimensions we can define e which determines the width of Areas A and B according to EN 1991-1-4 Figure 7.5.
For the case of e > d which is true for us, the width of Area A is defined as:
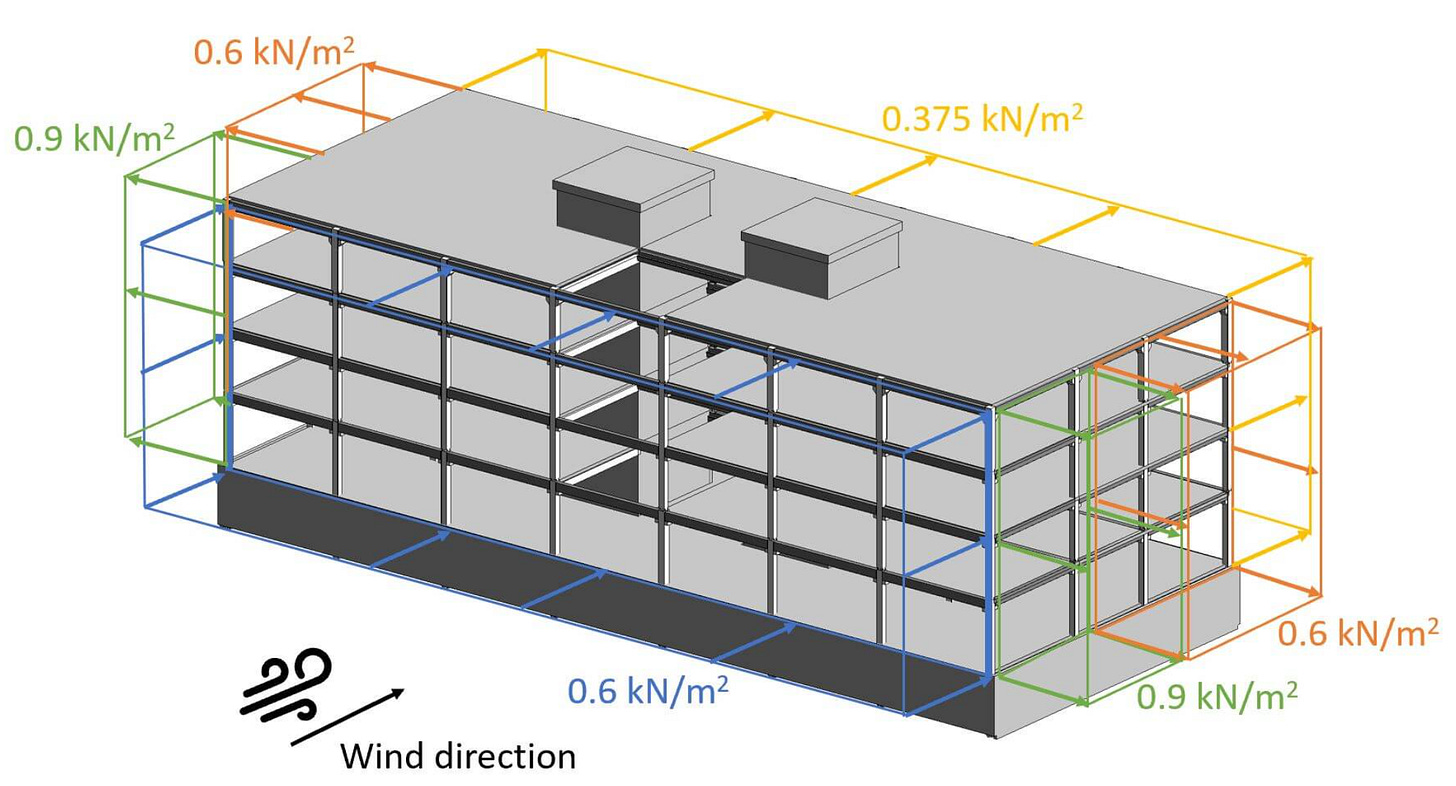
This leads to the following wind load areas. Note that in this case the width of the building is too little that there isn’t an area C.
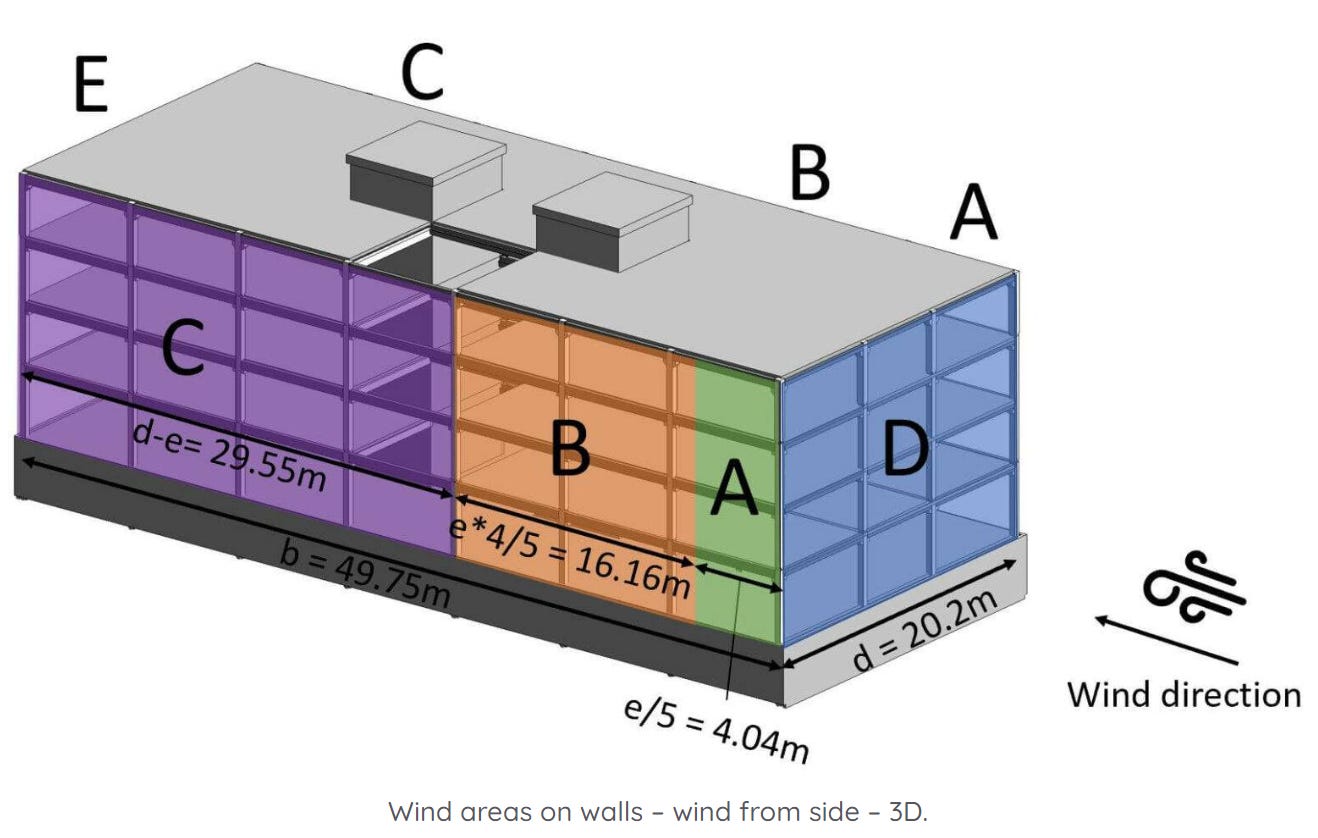
To better understand this, here’s a 3D representation of the wind load areas. The areas on the rooftop of the cores are not included due to better visualization. We also need to take them into account.
Now, let’s do the same for the longitudinal direction.
Wind in longitudinal direction
Width and length of the building (parameter d) for wind in longitudinal direction are defined as following:
From those dimensions we can define e according to EN 1991-1-4 Figure 7.5.
For the case of e < d which is true for us, the width of area A is defined as
The area B is calculated as
The area C is therefore the rest of d and calculated as
So let’s visualize all of those numbers.
#4 Find The External Pressure Coefficients From Eurocode
First, here’s the formula to calculate the characteristic wind load:
Where,
So, here in #4, we’ll find the values of cpe for the different wind load areas.
The coefficient cpe has 2 different values depending on the wind loaded area. There is value for a surface area of 1 m2 and 10 m2. These to values can also be written as
For the analysis of the overall stability of a building, we’ll use the external pressure coefficient for areas > 10 m2 (like in this newsletter). The value for surface areas of 1 m2 is used for small elements like roof tiles, parts of a facade, etc.
EN 1991-1-4 Table 7.1 gives recommendations for cpe. This means that you have to double-check with your National annex because those values might be defined differently there.
Pressure coefficients for wind in transverse direction
For a height to width ratio h/d = 17.1m/20.2m = 0.85 which is < 1 and > 0.25 we get the following coefficients.
Pressure coefficients for wind in longitudinal direction
For a height to width ratio h/d = 17.1m/49.75m = 0.34 which is < 1 and > 0.25 we get the following coefficients we get the same coefficients for A, B, D and E as for wind in transverse direction, but additionally we get now a value for C (EN 1991-1-4:2005 Table 7.1).
#5 Calculation Of The Wind Load
Based on the pressure coefficients, we found in #4 and the peak velocity pressure qp we can now calculate the wind load of the 5 wind areas.
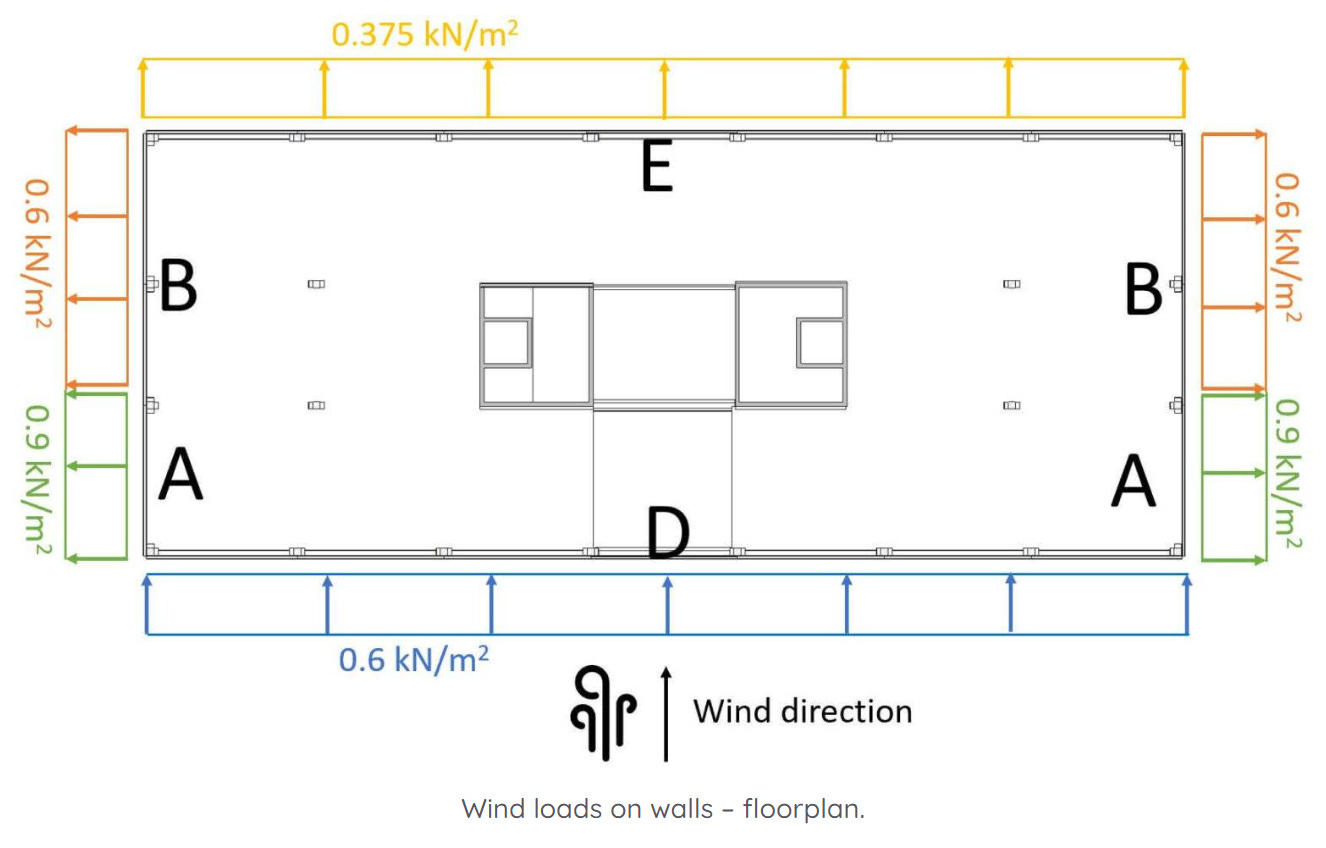
Transverse direction
When you calculate the wind loads the first time ever, it might be very confusing in which direction you have to apply the loads.
So let’s apply the wind loads (for 10 m2) on our building.
Longitudinal direction
Reduction of the wind load on areas D and E
According to EN 1991-1-4 7.2.2 (3) the wind loads can be reduced in the direction of the wind (Areas D and E) if they meet the following criteria:
Wind in transverse direction
The criteria are met, and the loads of areas D and E can be reduced by the factor 0.85.
Wind in longitudinal direction
The criteria are met, and the loads of areas D and E can be reduced by the factor 0.85.
Conclusion
For a building with the height of 17.1 m in a suburban area in Copenhagen, Denmark, the wind load on walls is calculated for 5 different areas and 2 wind directions.
Next week, we’ll check out how to calculate the wind load on roofs.
If you missed episode #1, #2, #3 or #4 of this new series, then you can find all previous posts → here ←.
Have a great rest of the week.
Until next Wednesday. 🙋♂️🙋♂️
Cheers,
Laurin. 😎😎
Enjoy the newsletter? Please forward to a friend you think could like our structural engineering content. It only takes 14 seconds. Making this one took a few hours. Just forward this link: https://www.structuralbasics.com/newsletter/