Supports & How To Calculate Their Reaction Forces
Post #4 of the Engineering Mechanics Series
Hi friends, 👋👋
In the last episodes we covered all the basics such as static systems, determinacy of beams and types of loads. Now we are ready to start calculating (finally). 🧮🧮 Today, we’ll look at how we calculate the reaction forces of static systems due to loads.
Next week, we’ll go a step further and calculate internal forces (normal and shear force and bending moment) based on loads and reaction forces.
So in this post we’ll first discuss what structural supports/reactions are, then we’ll present the different types of supports and finally show how we calculate their reaction forces.
Now let’s get into it. 🚀🚀
What are supports?
In short: Supports in structures make sure that the loads that are acting on the supported structure are getting transferred to the next element, like foundation, column, etc.
Here’s an everyday example:
This apple, for instance, is sufficiently supported by the table and that’s why it’s not moving somewhere. The word sufficiently plays a role here. Because as soon as the external loads acting on an element are bigger than the reaction forces that the support can take, the supports will fail, or the element will rotate or “slide away”. In the example of our apple, we only have to apply a small load on the side of the apple, and it will slide away.
Different types of supports
Every structure requires different supports, as the choice of support has a big influence on the behaviour of the structure. Due to supports, a structure can be restraint, flexible, rigid – not only because of the support, but it has a big influence. For example, the rigid frame as the name already says is quite rigid compared to the 2-hinge-frame which allows for much more deformation and deflection.
1. Pin support
The pin support has 2 reaction forces, a horizontal and a vertical. It’s used in simply supported beams, trusses, columns, frames, arches, continuous beams, etc.
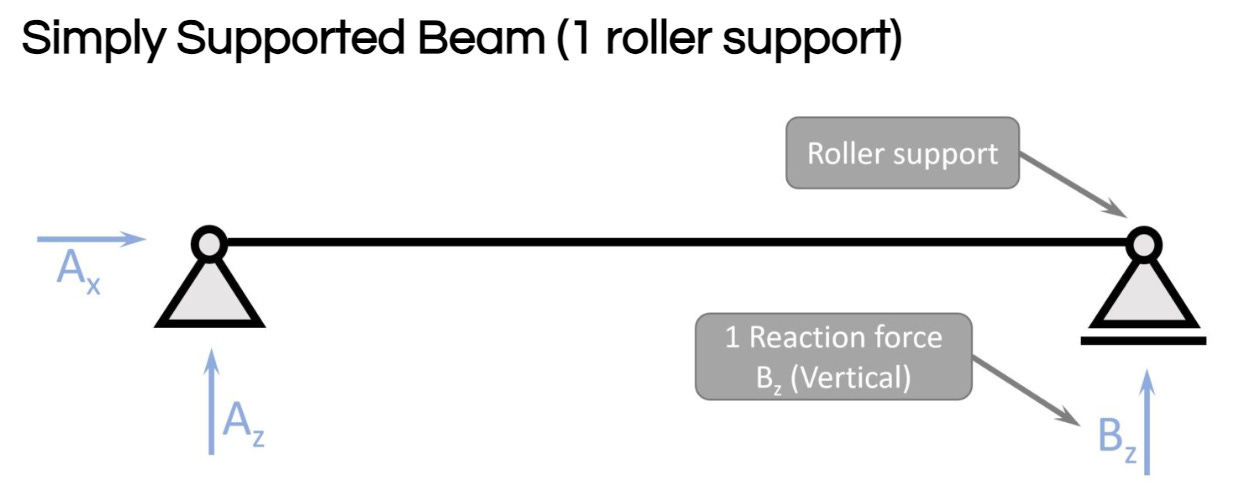
Roller support
The roller support has 1 reaction force, a horizontal or a vertical. It’s also used in simply supported beams, trusses, columns, frames, arches, continuous beams, etc.
Fixed support
The fixed support has 3 reaction force, a horizontal, a vertical and a moment. It’s also used in cantilever beams or rigid frames.
Spring support
Spring supports have 1 reaction force. However, the support could also be additionally restraint in another direction or rotation. Then you “add another” spring if the structure requires it. In the example of the cable stayed bridge (down below) the spring support behaves similar to a roller support. The main difference is that the spring support lets the deck (deflect) and the roller doesn’t.
OK, now let’s look at how we calculate the reaction forces of supports. 🔥🔥
How to calculate reaction forces
To calculate reaction forces, we first need to know whether the structure is statically determinate or indeterminate. In this newsletter, we’ll calculate the reaction forces of statically determinate structures. If you don’t know the difference, you can check out last week’s post or this article.
For statically determinate structures, the reaction forces can be calculated by the 3 Equilibrium equations.
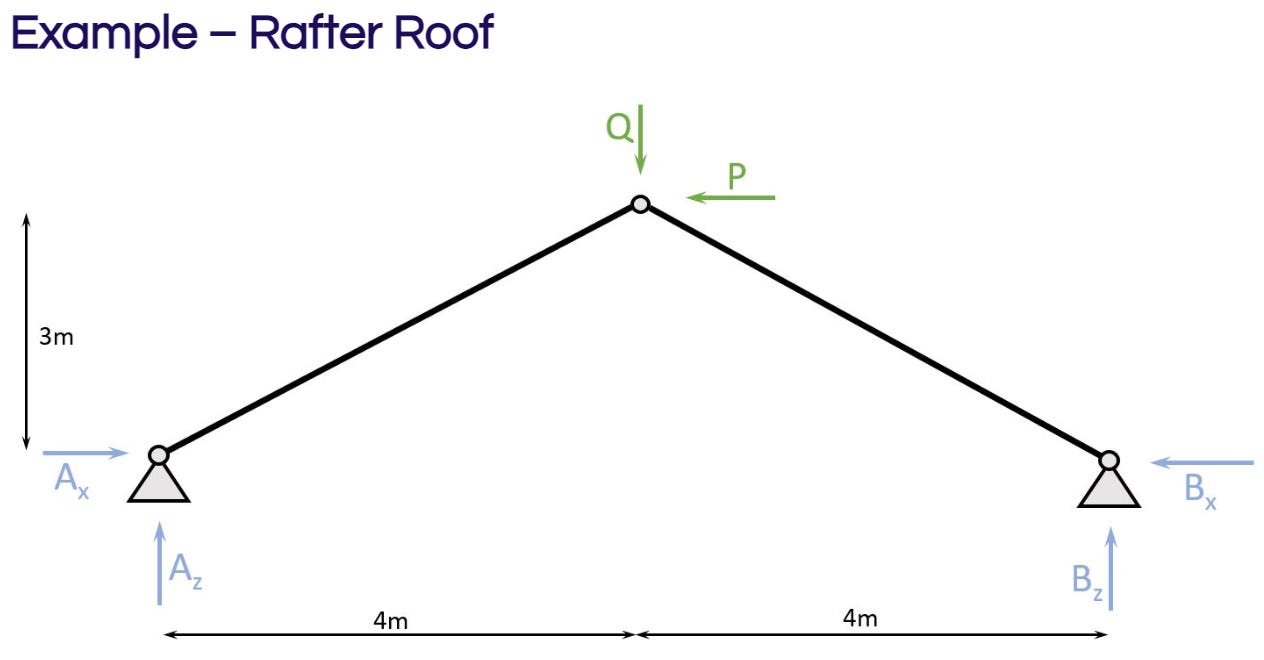
We’ll use the static system of a rafter roof to calculate the reaction forces. 👇👇
The chosen static system has 2 pinned supports A & B. Each of them have a horizontal and a vertical reaction force. 2 external forces Q – vertical point load – and P – horizontal point load – act on the static system.
Q = 2 kN, P = 3 kN
Let’s start by defining the 3 equilibrium equations.
The Moment in a specific point of a static system due to an external load is calculated as:
Moment = Load x Distance to a point
We are choosing to do the Moment equilibrium in point A.
The only equation where we just have 1 Unknown is the moment equilibrium. Therefore, we solve this equation first.
From here we can calculate Az with the vertical equilibrium.
To get the 2 horizontal reaction forces Ax and Bx we define another moment equilibrium in the top hinge but only considering the left beam.
Ax is inserted it in the horizontal equilibrium equation to get Bx.
We now successfully calculated all 4 support reaction forces. 🥳🥳
Conclusion
Calculating reaction forces is one of the first things you get introduced to at uni and as basic as this might be, it’s one of the most important fundamentals in structural engineering, which you’ll use in your entire uni and professional career.
This was already the 4th edition of this engineering mechanics series.
Hope to see you next Wednesday for another post. 😎😎
Have a great rest of the week. ✌️✌️
Cheers,
Laurin.

















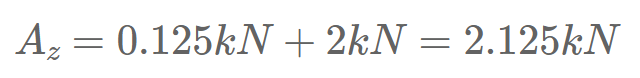

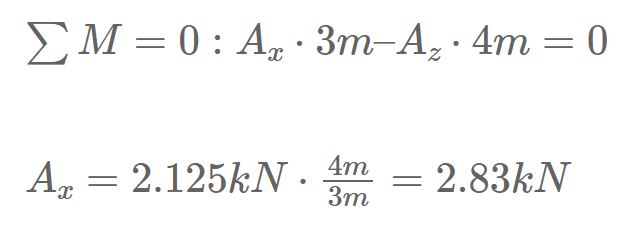


Great explanation. Thanks a lot.
Very simple and insightful. Love it